Research
Foundation Scientific Learning Models
Can we build a single large model for a wide range of scientific problems?
We proposed a new framework for scientific machine learning, namely “In-Context Operator Learning” and the corresponding model “In-Context Operator Networks” (ICON). A distinguishing feature of ICON is its ability to learn operators from numerical prompts during the inference phase, without weight adjustments. A single ICON model can tackle a wide range of tasks involving different operators, since it is trained as a generalist operator learner, rather than being tuned to approximate a specific operator. This is similar to how a single Large Language Model can solve a variety of natural language processing tasks specified by the language prompt. View the tutorial code in our GitHub repository.
We have a series of works on ICON.
- In our first paper, we proposed In-Context Operator Learning and In-Context Operator Networks. We showed how a single ICON model (without fine-tuning) manages 19 distinct problem types, encompassing forward and inverse ODE, PDE, and mean-field control problems, with infinite operators in each problem type. paper
- We evolved the model architecture of ICON to improve efficiency and support multi-modal learning, i.e., prompting the model with human language and LaTeX equations, apart from numerical data (See the following figure). paper
- We showed how a single ICON model can make forward and reverse predictions for conservation laws with different flux functions and time strides, and generalize well to PDEs with new forms, without any fine-tuning. We also showed prompt engineer techniques to broaden the capability of ICON. paper
- We proposed VICON, incorporating a vision transformer architecture to efficiently process 2D functions in multi-physics fluid dynamics prediction tasks. paper
![]()
Figure 1: Diagram for multi-modal in-context operator learning. The model learns the operator from the textual prompt and/or numerical examples, and applys to the question to make the prediction, with one forward pass.
![]()
Figure 2: Illustration of in-context operator learning for a mean-field control problem. The blue/red/black dots represent the data points in the prompt. The ICON model is able to learn the underlying operator from three examples and solve the problem with one forward pass.
Tracing the evolution of neural equation solvers, we see a three-act progression: Act 1 focused on approximating the solution function, e.g., Physics-Informed Neural Networks, while Act 2 shifted towards approximating the solution operator, e.g., Fourier Neural Operator, DeepONet. ICON can be viewed as an early attempt of Act 3, where the model acts like an intelligent agent that adapts to new physical systems and tasks.
Previous Works
Here are some of Yang Liu’s previous works during Ph.D. years:
– Bayesian Inference for PDEs with PI-GANs and B-PINNs
This series of works aim to address the following challenge: How to perform stochatic modeling and uncertainty quantification for physical systems, with the knowledge of the governing equations and scattered/noisy measurements?
To accurately model the distribution within physical systems (typically defined within a functional space) we proposed Physics-Informed Generative Adversarial Networks (PI-GANs). This method effectively integrates physical principles and data, making it suitable for modeling stochastic physical systems or for learning prior distributions from historical data. When combined with our proposed Bayesian Physics-Informed Neural Networks (B-PINNs), which establish likelihoods based on governing equations and observational data, this framework allows for systematic Bayesian inference on PDEs.
– Learning Optimal Transport Map and Particle Dynamics
Being the first to draw the connection between deep generative models and the continuous flow formulation of optimal transport, we proposed potential flow generator as a plug-and-play generator module for different GANs and flow-based models. With a special ODE-based network architecture and an augmented loss term tied to the Hamilton-Jacobi equation derived from the optimal transport condition, the potential flow generator not only transports the source distribution to the target one, but also approximates the optimal transport map.
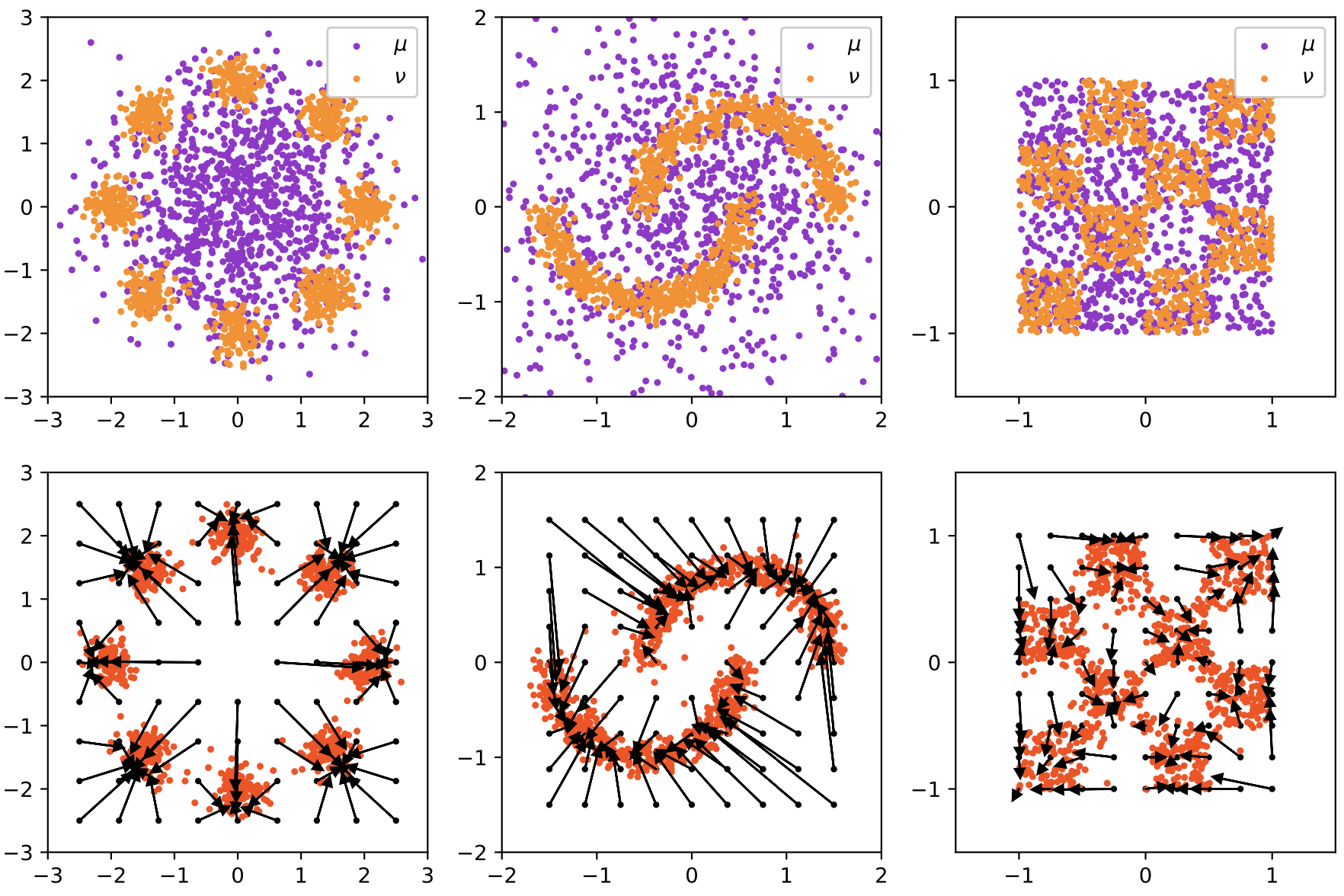
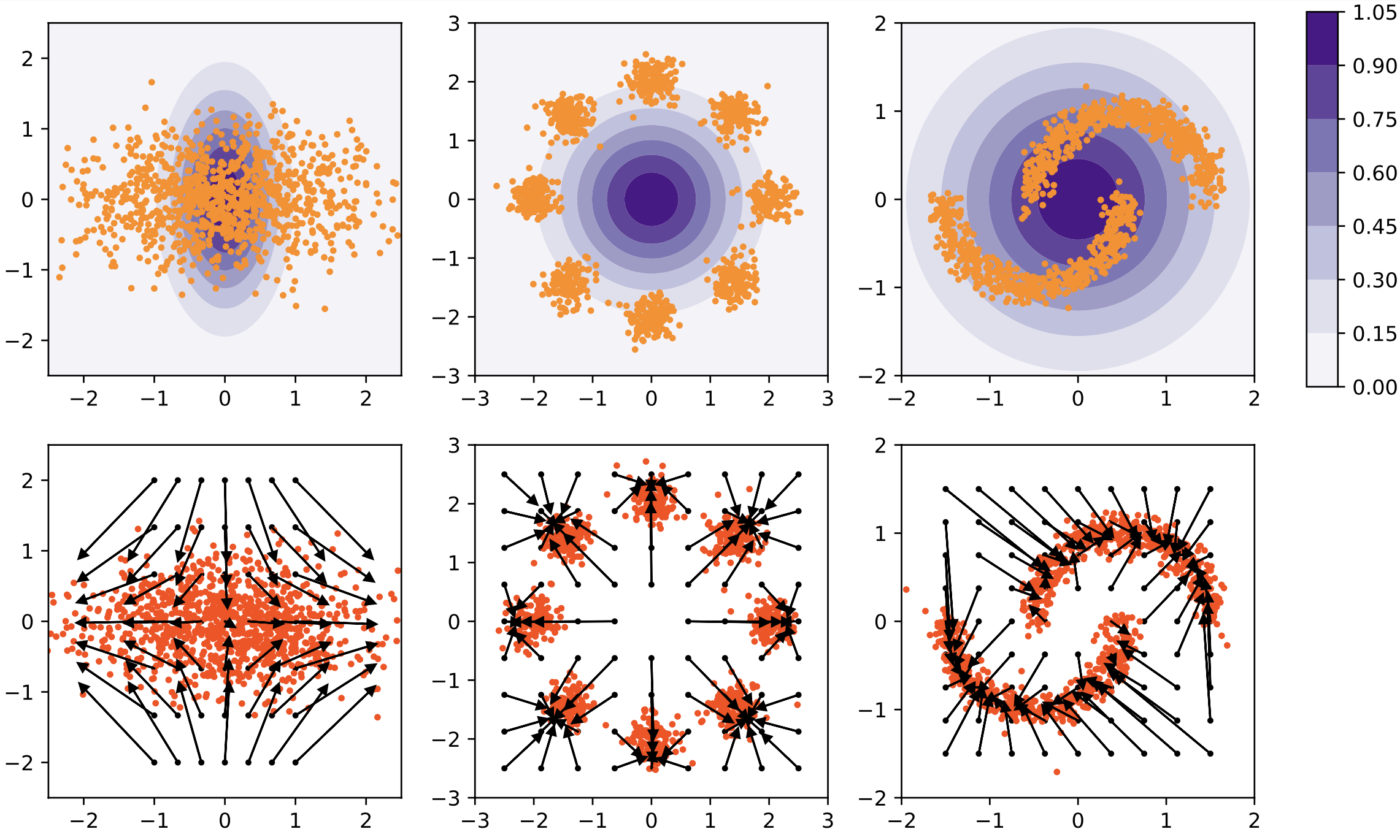
Potential flow generator in GANs (left 3 columns) and normalizing flow (right 3 columns). The first row shows the samples or the unnormalized densities of source distributions \(\mu\) (in purple) and target distributions \(\nu\) (in orange), the second row shows the learned optimal transport maps \(G\) and the push forward distributions \(G_{\#}\mu\).
Subsequently, we extended this framework to inference of particle dynamics from paired/unpaired observations of particles, encompassing non-local particle interactions and high-dimensional stochastic particle dynamics.
These works were cited by other great works in high-dimensional mean-field problems, single-cell transcriptomics, and flow matching for generative modeling.
… and more